Vaak zegt men dat mensen, als lineaire denkers, niet overweg kunnen met exponentiële verandering in technologie omdat die beide curves niet overeenkomen en een verschillende snelheid of groei kennen. Mensen kunnen maar één lineaire stap tegelijk zetten, terwijl de snelheid van nieuwe technologieën met elke stap verdubbelt. Zo wil men ons laten geloven dat er geen verband is tussen lineair denken en exponentiële verandering.
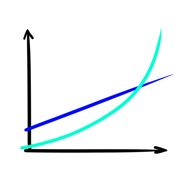
Maar als we kijken naar wiskunde, dan komen een exponentiële curve en een lineaire curve wél overeen. Ooit gehoord van de eerste afgeleide? Wel, de eerste afgeleide van een exponentiële curve is… een lineaire curve. Dat betekent dat we voor elk punt op een exponentiële curve een lineaire curve kunnen vinden die er rakelings langs loopt.
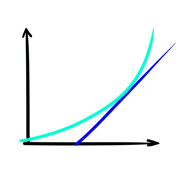
Wikipedia zegt zelfs: “De afgeleide van een functie van een echte variabele meet de gevoeligheid voor verandering van de functiewaarde (outputwaarde) t.o.v. de verandering in het argument (inputwaarde). Afgeleiden zijn een fundamenteel instrument van berekening.” Het meten van de gevoeligheid voor verandering is waarom wij, als lineaire denkers, stress voelen bij deze nieuwe technologieën.
Maar hoe helpt deze theorie ons om over te gaan tot exponentieel denken?
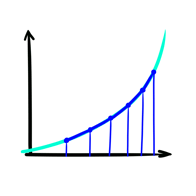
In de begindagen van de computer wilden we berekeningstijden verkorten, dus we programmeerden computers zodat zij complexe berekeningen voor ons konden maken. Het berekenen van complexe vormen was een tijdrovende bezigheid, dus zochten we hulp bij computers. In de begindagen van de computer noemden we dit trouwens de ‘eindige-elementenmethode’.
Met eindige elementen splitsen we een complexe vorm of curve op in kleine oneindige stappen. We beschouwen elk element als een lineair element en berekenen de best passende rechte als een alternatief voor de oneindige kleine curve.
Dus moeten we hetzelfde doen met de exponentiële veranderingen. Als we de technologie beetje bij beetje benaderen, en in kleine, lineaire stappen leren wat die stukjes betekenen, hoe ze ons kunnen helpen, wat ze voor onze business kunnen doen… dan kunnen we gestaag groeien en de exponentiële veranderingen van technologieën bijbenen.
Natuurlijk is het niet mogelijk om alle technologieën tegelijkertijd aan te pakken, maar we mogen niet aarzelen met hun implementering. Deze technologieën zijn er om ons slimmer te maken, ons te helpen groeien en nieuwe business of nieuwe kansen te grijpen.
Eigenlijk moeten we deze technologieën zien als rekenmiddelen, bedoeld om ons sneller en slimmer te helpen nadenken.
Dus hoe kunnen we als lineaire denkers de stap maken naar exponentieel denken en onze denksnelheid verhogen?
Als we de basisbeginselen van de lineaire curve nemen, dan zijn er 2 mogelijkheden om de kennisratio te vergroten. Ofwel vergroten we b, de Y-asafsnede, of we vergroten a, de richtingscoëfficient van de curve.
In een exponentieel veranderende wereld betekent het vergroten van ‘b’ dat we nieuwe technologieën implementeren als nieuwe vaardigheden, nieuwe mogelijkheden om sneller te denken.
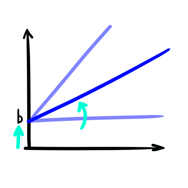
In diezelfde wereld kunnen we ‘a’ vergroten, de richtingscoëfficient van onze lineaire denkcurve, door deze nieuwe technologieën te vertrouwen omdat we geloven dat ze ons in de toekomst zullen helpen om sneller te denken. Door daarin te geloven gaan we mee in de verandering die ze teweeg brengen, dus een kleine lineaire stap zal hoger eindigen dan voorheen.
Voor mij gaat hybride denken hierover: het verkennen en aanvaarden van, en experimenteren met nieuwe technologieën en ze gebruiken als rekenmethodes die ons toelaten sneller te denken.
Misschien dat de technologie ooit in onze hersenen kan worden ingeplant zodat de connectie met het denken compatibel wordt, maar tot die tijd kunnen we enorme vooruitgang boeken door deze nieuwe technologieën en vaardigheden onder de knie te krijgen.
Eigenlijk is het grappig te bedenken dat we deze methodologie gebruikten om onze computers te programmeren en dat deze expontentieel zijn gegroeid, terwijl wij als mensen vergeten zijn deze methode toe te passen op ons eigen denkproces. Maar er is nog tijd om de schade in te halen...
Wil jij (jouw business) evolueren richting exponentieel denken?



